Understanding Triads (Chords)
A chord can be defined as a group of two or more harmonizing notes.
The most basic and common formation of a chord, a triad, is a group of three harmonizing notes in which an interval of a third and an interval of a fifth is played above the root note.
Now, there are two different types of thirds and two different types of fifths which are used when constructing triads.
The first type of third we need to know about is called a Major third. A Major third is constructed by adding two consecutive whole steps above or below a given note.

For example, knowing that C to D is a whole step,
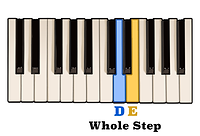
and D to E is also a whole step,
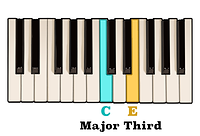
then C to E having been two consecutive whole steps is a Major third.
A minor third, on the other hand is constructed by adding a half step and a whole step above or below a given note.
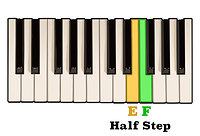
Again, knowing that E to F is a half step,
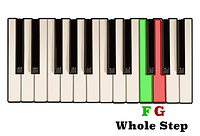
and F to G is a whole step,

then E to G, having been a half step followed by a whole step, is a minor third.
The first type of fifth that we need to know about is called a Perfect fifth. A Perfect fifth fifth is constructed by adding a Major third and a minor third above or below a given note.

We just learned that C to E is a Major third,

and E to G is a minor third.
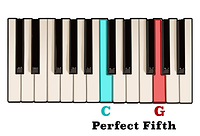
Therefore, C to G, having been a Major third followed by a minor third is a Perfect fifth.
The second type of fifth is known as a diminished fifth. A diminished fifth is constructed by adding two consecutive minor thirds above or below a given note.

If we know that B to D is a minor third,

and E to and D to F is also a minor third,
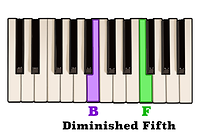
then B to F, having been two consecutive minor thirds is therefore a diminished fifth.
It’s worth mentioning that another even easier way of thinking about diminished fifths is that they are the same as perfect fifths just lowered by one half step.


A Major triad is formed by adding a Major third and a Perfect fifth above the same note.

By playing a Major third above the note C,

along with a Perfect fifth above the note C,

we will have constructed a C Major triad - C, E, and G.
Another way to construct a C Major triad is by combining the first, third, and fifth scale degrees of a C Major scale.

Here we can see that the first scale degree is the note C, the third scale degree is the note E, and the fifth is G.
A minor triad is formed by adding a minor third and a Perfect fifth above the same note.
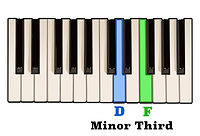
By playing a minor third above the note D,

along with a Perfect fifth above the note D,

we will have constructed a D minor triad - D, F, and A.
Another way to construct a D Major triad is by combining the first, third, and fifth scale degrees of a D minor scale.
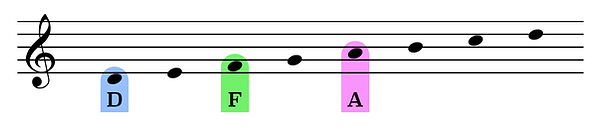
Here we can see that the first scale degree is the note D, the third scale degree is the note F, and the fifth is A.
A diminished triad is formed by adding a minor third and a diminished fifth above the same note.

We already know that the note D is a minor third away from B,

and F is a diminished F away.

By combining these three notes we will be playing a B diminished triad.
Each note of a Major scale can be considered the root note of a different triad.
For example, triads built on the first, fourth, and fifth scale degrees will always be Major.

Triads built on the second, third, and sixth scale degrees will always be minor.

And a triad built on the seventh scale degree is diminished.


